Det kan göras! Kom ihåg att en överföringsledning består av viss självinduktans per längdenhet och en del kapacitans per längdenhet, och förhållandet mellan dessa bestämmer linjens karakteristiska impedans:
$$ Z_0 = \ sqrt {\ frac { R + j \ omega L} {G + j \ omega C}} $$
Intuitivt då kan en klumpad elementimplementering se ut som någon serieinduktans och någon parallell kapacitans. Vi behöver något som är symmetriskt, så ett pi-nätverk 1 som detta borde göra det:

simulera denna krets - Schemat skapat med CircuitLab
Allt vi behöver göra är att bestämma lämpliga värden. Eftersom överföringsledningar fungerar i båda riktningarna kommer detta arrangemang att vara symmetriskt, så C1 = C2. Och som det visar sig är värdena mycket eleganta: komponenternas reaktans är lika med den karakteristiska impedansen. Sätt matematiskt:
$$ X_ {L1} = Z_0 \\ X_ {C1} = Z_0 $$
Och medan vi håller på med det, låt oss granska formlerna för reaktans:
$$ X_L = 2 \ pi f L \\ X_C = 1 / (2 \ pi f C) $$
Att sätta ihop dem, med lite algebra, får du:
$$ L = {Z_0 \ över 2 \ pi f} $$
$$ C = {1 \ över 2 \ pi f Z_0} $$
Låt oss säga att vi vill ha en karakteristisk impedans på 86,6 ohm så att vi kan förverkliga en 3-vägs Wilkinson-effekt delare. Vi använder frekvensen 435 MHz för mitten av 70 cm-bandet.
$$ L = {86.6 \: \ Omega \ över 2 \ pi \ cdot 435 \: \ mathrm {MHz}} = 31.5 \: \ mathrm {nH} $$
$$ C = {1 \ över 2 \ pi \ cdot 435 \: \ mathrm {MHz} \ cdot 86.6 \: \ Omega} = 4.22 \: \ mathrm {pF} $$
Så nu är kretsen med verkliga värden avslutad med en belastning på 86 ohm:
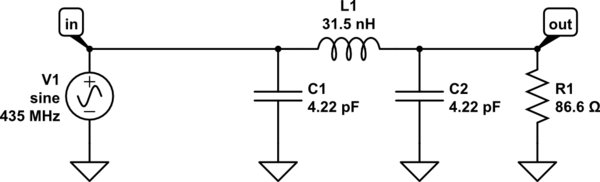
simulera den här kretsen
Om detta verkligen är en kvartvågs överföringsledning, bör vi se R1 90 grader ur fas med ingången. Låt oss köra en tidsdomän-simulering:


Bingo! De impedantomvandlande egenskaperna för en kvartvågstransmissionsledning bevaras också: om utgången är öppen kommer källan att se en kort, och så vidare. Så denna krets kan användas på plats var som helst som kräver en kvartvågs överföringsledning.
1 Detta pi-nätverk gör ett lågpassfilter, vilket kan vara ett fin bieffekt eftersom det minskar harmonisk distorsion.