Du väcker en utmärkt fråga och dina tankeprocesser är verkligen på rätt väg.

Först lite bakgrund. En idealisk, oavbruten sinusformad bärare har noll bandbredd. Verkliga faktorer som fasbrus, förstärkare förvrängning etc. ger en mätbar bandbredd hos bäraren. När bäraren slås på och av som med Morse-kod är detta en speciell form av ASK (Amplitude Shift Keying) som heter OOK (On Off Keying) som det diskuteras i professionell litteratur. Normalt minimeras bandbredden för den modulerade OOK-signalen när nyckelvågformens stignings- och falltider har en Gaussisk eller upphöjd cosinusform. De flesta amatörradiosändtagare använder enklare RC-filtrering för att forma nyckelvågformen, vilket resulterar i mindre än ideal bandbredd men åtminstone undviker tangentklick från den annars skarpa höjnings- och falltiden för moduleringssignalen. I vilket fall som helst är det stignings- och fallformen för den nyckelformade vågformen som bestämmer bandbredden för den modulerade signalen.

När övergången för den modulerande signalen synkroniseras med nollkorsningen av bärarsignalen är känd som sammanhängande OOK-modulering . Detta är naturligtvis mycket svårare att implementera än ett enkelt, icke-sammanhängande RC-filtreringsschema så det ses inte vanligt i amatörradioapplikationer. Emellertid minskar, men eliminerar, inte signalbandbredden när den implementeras korrekt koherent OOK. Den "återstående" bandbredden beror till stor del på en mängd verkliga faktorer inklusive icke-ögonblicklig nyckeltid som inför en förvrängning av bärvågens form. Varje distorsion, oavsett hur liten, den sinusformade bäraren kommer att leda till en bandbredd som inte är noll.

[EDIT] Även med ideal nollkorsningsomkoppling och idealförstärkning kommer det att finnas mindre sidoband men dessa kommer att rulla av som en funktion av frekvensen i en betydligt högre takt än att byta vid icke-nollpunkter. Med nollkorsningsomkoppling kommer emellertid icke-linjär förstärkning som finns i de flesta CW-sändare troligen att introducera större sidobandkomponenter än de som orsakas av nollkorsningsomkoppling. [/ EDIT]

Så du kan vinna över några av CW-fansen med en sammanhängande OOK-sändare, men på en hobbymarknad skulle en sådan sändares kommersiella lönsamhet vara en fråga om priselasticitet. Kanske i denna nya era av DSP-baserade radioapparater kommer de sänkta kostnaderna för implementering att göra detta kommersiellt lönsamt. Men med tanke på att få, som Elecraft K3, amatörradiosändtagare implementerar Gaussian keying, har vi fortfarande ett sätt att gå för att optimera bandbredden för våra CW-signaler.

Det finns inget sätt att överföra information i en signal med noll bandbredd. Att byta bärare vid nollgenomgångarna skulle minska bandbredden men inte ta den till noll.

Det finns en matematisk förklaring på DSP StackExchange: Minskar det att "tända" en sinusvåg vid en nollgenomgång bandbredd? Sammanfattning: i värsta fall av att slå på / av vid den maximala momentana amplituden faller sidobanden av i proportion till 1 / f. I bästa fall att byta vid nollgenomgångar är andelen 1 / f ² . En betydande förbättring, men ändå långt ifrån noll bandbredd!

Utan att fördjupa sig i matematik är den enkla förklaringen att en bandbegränsad signal inte bara måste vara kontinuerlig i sig, utan också dess derivat. En hård omkopplare vid nollgenomgång har en diskontinuitet i det första derivatet vid omkopplingspunkten.

För att ha släta derivat är Gauss-funktionen ett begränsande fall eftersom derivatet av en Gaussisk funktion är en annan Gaussisk. Den Gaussiska funktionen kommer upp i centralgränssatsen av liknande skäl.

Det är i allmänhet sant att att lösa något exakt i tidsdomänen kräver en bred bandbredd och vice versa, och den Gaussiska funktionen är en "mellanliggande mark" som maximerar uppgångs- och falltiderna samtidigt som sidobanden minimeras i den mån det är matematiskt möjligt. Detta beror på att Fourier-transformationen av en Gaussian är en Gaussian. Så i det avseendet skulle det minimala nyckelkuvertet för bandbredd för CW vara en Gaussisk funktion.

De "koherenta CW" -folket använder något liknande.

Mycket långsam CW är nycklad vid nollkorsningar med höjt Cosine-kuvert för att ge minimal bandbredd.

Men ja, det är uppgångs- och falltiderna som ger nyckelklick, inte om det är tangent vid noll korsningar eller inte

Rob Sherwood NC0B från Sherwood Engineering Inc. gjorde en undersökning och producerade en video som visade att stigningstiden (och förmodligen också falltiden) är nyckeln till att minska bandbredd. Han jämförde stigningstider på 1 ms till 10 ms. För snabb ökningstid ökar bandbredden avsevärt. För att svara på Dominicks fråga tittade jag på CTU-filerna (Contest University). Rob har nämnt detta i nästan alla hans presentationer varje år han har talat. De finns i filmerna här eller filerna här.

För det första finns det inget som heter en signal med noll bandbredd. Det är som den imaginära linjen mellan två imaginära punkter - linjen utan bredd mellan punkter utan storlek.

Det är som att säga isotrop antenn. (En FCC-favorit)

Det finns helt enkelt inga sådana saker förutom som teoretiska konstruktioner - slutar även då, för att förhindra att dela med noll, måste de alltid uttryckas som gränser för variabler när de närmar sig noll.

CW-sändare börjar alltid vid nollutgång (vad du kallar en nollkorsning, men vid gränsförhållandet) tills de är befallda att producera en signal genom att stänga en kontakt på en nyckel eller på annat sätt. Sedan återgår de till noll när det utgående kommandot tas bort.

CW-sändare kommer inte direkt till full effekt och producerar vågformer så här:

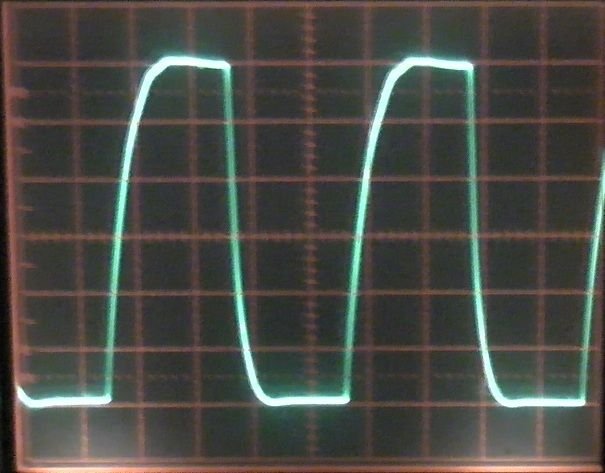
Observera att eftersom detta visas i tidsdomänen relativt nyckelfrekvensen är den faktiska bäraren inte synlig.

Så även om moduleringen i sig (nyckeln, fungerar som en omkopplare) är en fyrkantig våg , är den resulterande utgången inte riktigt fyrkantig på grund av de fysiska begränsningarna hos sändarens komponenter.

Detta gäller både kuvertets uppgång och nedgång.

Här är ett annat exempel:

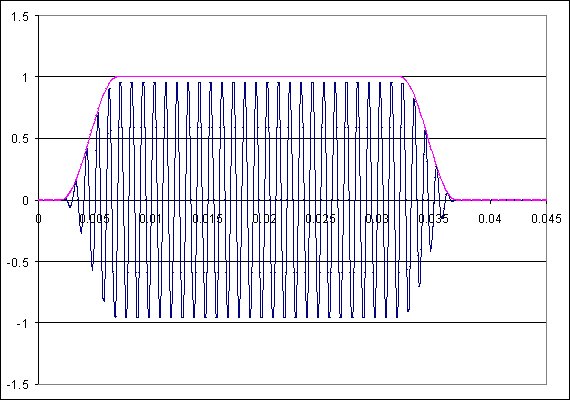
I denna kurva, i förhållande till bärfrekvensen, framgår det tydligt att i praktiskt avseende det sända våghöljet verkligen börjar och slutar vid gränsvillkoren noll.

Naturligtvis har filosofer varit kända för att hävda att det aldrig når noll - det kommer bara närmare och närmare. Sedan tar kvantfysikerna upp Planck-gränserna, och så vidare, illamående.

På frekvensdomänen kommer det att se ut så här:

Observera att detta är en plot av en signal modulerad av 1 KHz fyrkantvågor, varför bandbredden sprids så vida. Vid 1 KHz-nyckling når förhållandet mellan signal och moduleringsfrekvenser till den punkt där det producerar sidoband. Sidobandens amplituder faller av på normalt sätt. Denna plot visar inte effekterna av ingångsfiltrering.

Tänk på en generisk blandarkrets - utgången ska alltid filtreras på ett sådant sätt att endast den önskade modulerade bäraren är den resulterande utgången.

Risetime-delen är som om den har modulerats med mycket hög hastighet. Det ger falska utsläpp i förarkretsen som sedan filtreras bort. De ska inte ligga inom den slutliga effektförstärkarens bandpass.

Men eftersom inget filter är perfekt kommer några av dessa sporrar att hamna på utdata. Därav behovet av riktlinjer för begränsning av falska utsläpp. Dessa regleras specifikt för FCC-typaccepterade kommersiella sändare.

I slutändan vill du ha en sändare som uppvisar högre Q som ett mått på hur väl den tillämpar tillgänglig effekt på önskad utfrekvens för högre effektivitet.

Här är en intressant artikel om ämnet (lite TL; DR):

Effekt av nyckelvågform på CW-bandbredd

EXCERPT:

överföringsfunktionen för en riktig sändare är INTE linjär.

dvs en fyrkantvågsingång (där stigningstiden och nedgångstiden är som om frekvensen av modulering är vid gränsvillkoren för gränsen för att den är i oändlighet, där gränsen för moduleringsperioden närmar sig noll.

Slutsatsen är att eftersom det inte finns någon bärare mellan Morse element börjar utgången alltid vid noll och slutar med noll.

Handnyckling sker i så långsam takt jämfört med bärvågsfrekvensen att den inte är särskilt relevant.

O-scope-spåret längst upp är hämtat från en sändare på 630 meter, och även då är moduleringshastigheten fortfarande så långsam jämfört med till och med den låga bärfrekvensen att det inte finns några tydliga artefakter införda genom nyckel i slumpmässig tid relativ till bärarens svängningar.

Det är moduleringsfrekvensen som är den dominerande faktorn för att producera den slutliga signalbandbredden.

Som en åtminstone, tillbaka den dagen då FCC hade övervakningsstationer överallt, besökte jag ibland och tittade när de använde det de kallade "TXID" - sändaridentifiering - hur en signal från en CW- eller FM-sändare vandrar i frekvens och amplitud som de var knappade upp. De var väldigt bra på detta och kunde ofta berätta vem som sände innan någon identifierande modulering tillämpades. det vill säga att säga eller knappa ett kallsignal.

De berättade för mig att även med samma modeller av sändare som tillverkades på samma produktionslinje samma dag skulle det finnas mätbara skillnader på grund av toleranserna för de olika komponenterna som ingick i slutprodukten. De ansåg att detta var nära hållen information vid den tiden.

Från en matematisk synpunkt har varje signal med begränsad längd (t.ex. nyckel) oändlig bandbredd. Du kan minska sidobanden genom att välja ett nyckelhölje vars FT har låga sidoband, vilket innebär att kuvertets långsamma uppgång / falltider och i minskande grad alla dess derivat.